ผมขอนำเสนอวิธีการวิเคราะห์วงจรไฟฟ้ากระแสตรงแบบใหม่ ซึ่งแตกต่างจากวิธีการที่ผม(และอีกหลายคน)เคยเรียนกันมาในวิชาฟิสิกส์ ผมได้วิธีการนี้มาจากบทความเรื่อง “Electric Circuits: A New Approach — Part 1” ครับ แต่ก่อนอื่น ผมต้องขอเรียนก่อนว่า วิธีการนี้อาจใช้ได้กับวงจรไฟฟ้ากระแสตรงธรรมดาๆ ที่ไม่มีตัวเก็บประจุไฟฟ้าและขดลวดเหนี่ยวนำนะครับ วิธีการนี้จึงเหมาะกับการสร้างความเข้าใจพื้นฐานเกี่ยวกับวงจรไฟฟ้ากระแสตรงให้กับนักเรียนชั้นมัธยมศึกษาครับ
โดยปกตินั้น เวลาเราจะวิเคราะห์วงจรไฟฟ้ากระแสตรง เราก็ต้องใช้หลักการอยู่ 3 ข้อ ซึ่งก็คือ (1) กฎของโอห์ม (2) กฎของเคอร์ชอฟ และ (3) หลักการรวมความต้านทาน (ทั้งแบบอนุกรมและแบบขนาน) สิ่งเหล่านี้เป็นเหมือนหลักการที่เราต้องยึดถือในการวิเคราะห์วงจรไฟฟ้า และคำนวณหาค่าปริมาณต่างๆ ในวงจรไฟฟ้า ซึ่งอยู่ในรูปของการใช้สมการต่างๆ เช่น V = IR, Iเข้า = Iออก, Rรวม = R1 + R2 + … (สำหรับการต่อตัวต้านทานแบบอนุกรม), และ 1/Rรวม = 1/R1 + 1/R2 + … (สำหรับการต่อตัวต้านทานแบบขนาน) วิธีการนี้อาจมีข้อจำกัดหน่อย โดยเฉพาะสำหรับนักเรียนที่ไม่ถนัดการใช้สูตรคำนวณ นักเรียนจำนวนหนึ่งไม่สามารถเห็นความสัมพันธ์ระหว่างส่วนต่างๆ ของวงจรไฟฟ้าได้ทั้งหมดพร้อมกัน ทั้งนี้เพราะนักเรียนต้องคำนวณไปทีละจุดๆ
วิธีการใหม่นี้จะช่วยให้นักเรียนเห็นภาพความสัมพันธ์ของส่วนต่างๆ ในวงจรไฟฟ้าใดๆ ได้ง่ายและเป็นรูปธรรมมากขึ้นครับ โดยเราสามารถใช้แผนภาพรูปสี่เหลี่ยมแทนตัวต้านทานแต่ละตัว และใช้หลักการของการหาพื้นที่ของสี่เหลี่ยมในการคำนวณหาค่าปริมาณต่างๆ ตัวอย่างเช่น เราสามารถใช้สี่เหลี่ยมแทนตัวต้านทาน ดังนี้
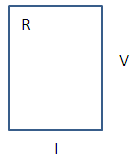โดยเราจะเขียนค่าความต้านทานไว้ที่มุมบนด้านซ้ายมือ เขียนค่าความต่างศักย์ไฟฟ้าที่ตกคร่อมตัวต้านทานนี้ไว้ที่แนวตั้งด้านซ้ายมือ และเขียนค่ากระแสไฟฟ้าที่ผ่านตัวต้านทานนี้ไว้ที่แนวนอนด้านล่าง ในที่นี้ ผมเขียนเป็นตัวแปร (R, V, และ I) ไว้ก่อน เดี๋ยวพอเรารู้ค่าของตัวแปรเหล่านี้จากที่โจทย์กำหนดไว้ หรือจากที่เราคำนวนได้ เราก็ค่อยๆ มาใส่เติมลงไปครับ
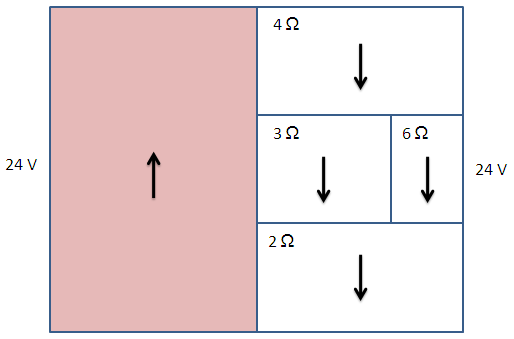
หลักการของวิธีการนี้คือว่า เมื่อตัวต้านทานต่อเข้ากันเป็นวงจรไฟฟ้าแล้ว แผนภาพสี่เหลี่ยมต้องประกบเข้ากันเป็นรูปสี่เหลี่ยม(ที่มีขนาดใหญ่ขึ้น)ได้พอดี โดยไม่มีช่องว่างระหว่างกันและไม่มีการซ้อนทับกัน เราลองมาดูตัวอย่างจากโจทย์กันนะครับ (โจทย์ข้อนี้กำหนดให้นักเรียนหาค่ากำลังไฟฟ้าที่สูญเสียไปกับตัวต้านทาน 3 Ω ) วงจรไฟฟ้าเป็นดังนี้
ที่มา: http://www.vcharkarn.com/
เราก็แปลงวงจรไฟฟ้านี้ให้เป็นแผนภาพ ซึ่งจะได้ผลดังนี้ครับ
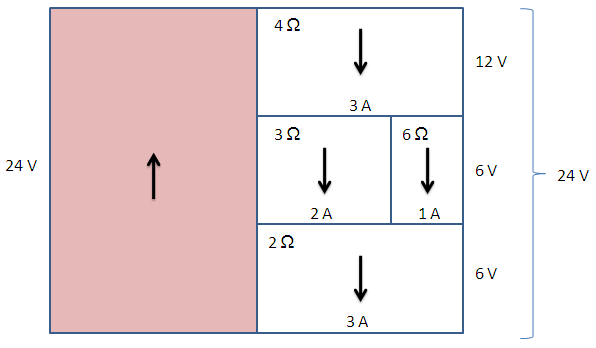
แผนภาพนี้ประกอบด้วย 2 ส่วน ซึ่งประกอบด้วยส่วนด้านซ้าย (สีแดง) และส่วนด้านขวา (สีขาว) [เราอาจจินตนาการว่า มันคือหนังสือที่เปิดกางอยู่ก็ได้ครับ] ส่วนสีแดงนั้นแทนแรงเคลื่อนไฟฟ้าที่แบตเตอรี่จ่ายให้กับวงจรไฟฟ้า ซึ่งเราได้ข้อมูลจากโจทย์ว่า มันมีค่าเท่ากับ 24 V ดังนั้น ความต่างศักย์ที่ตกคร่อมวงจรไฟฟ้านี้ทั้งหมดจึงมีค่าเท่ากับ 24 V ด้วย ซึ่งสอดคล้องกับกฎของสี่เหลี่ยมผืนผ้าที่ด้านฝั่งตรงข้ามต้องมีความยาวเท่ากัน
ส่วนสีขาวนั้นแทนวงจรไฟฟ้า ซึ่งประกอบด้วยตัวต้านทาน 4 ตัว การต่อตัวต้านทานแบบอนุกรมจะปรากฏในแผนภาพในรูปแบบของการเรียงลำดับจากบนลงล่าง ในขณะที่การต่อตัวต้านทานแบบขนานจะปรากฏในแผนภาพในรูปแบบของการเรียงลำดับจากซ้ายไปขวา
ลูกศรในสี่เหลี่ยมแต่ละอันนั้นแทนทิศของกระแสไฟฟ้า (ซึ่งไม่จำเป็นในการคำนวณหาค่าต่างๆ แต่ผมใส่เข้ามาเพื่อให้การสื่อสารตรงกันครับ) เนื่องจากกระแสไฟฟ้าไหลจากขั้วบวกไปยังขั้วลบ ดังนั้น ลูกศรในส่วนสีแดงจะมีทิศขึ้น ส่วนลูกศรในส่วนสีขาวจะมีทิศลง
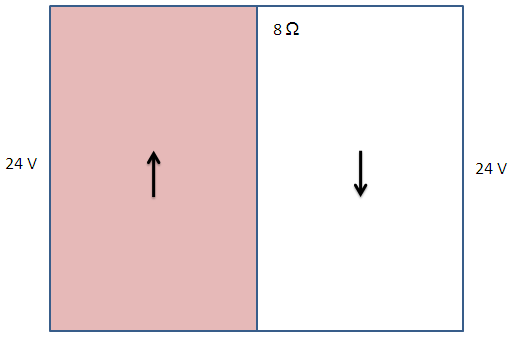
จากนั้น เราอาจจำเป็นต้องใช้ความรู้เกี่ยวกับการรวมค่าความต้านทานนิดหน่อย โดยเราอาจจะเริ่มจากการรวมค่าความต้านทาน 2 ตัว (3 Ω และ 6 Ω) ที่ต่อขนานกันก่อน ซึ่งจะได้เท่ากับ 2 Ω [อันนี่ ผมขอละไว้นะครับ ครูฟิสิกส์จะเข้าใจดี] จากนั้น เราก็รวมค่าความต้านทานทั้งหมด (ซึ่ง ณ ตอนนี้ต่ออนุกรมกัน) ได้เท่ากับ 8 Ω เราก็อาจเขียนแผนภาพสรุปหลังจากการรวมค่าความต้านทานให้เสมือนว่าเป็นตัวต้านทานเดียวกันแล้วได้ ดังนี้
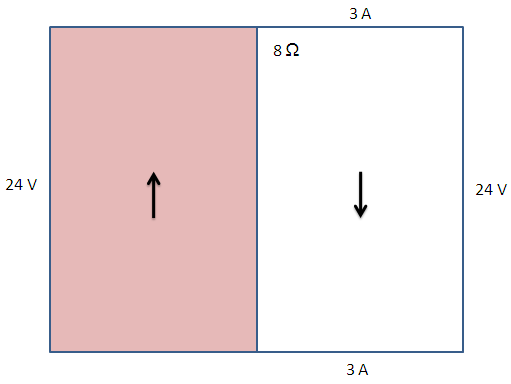
จากนั้น เราก็ค่อยคำนวณหาค่ากระแสไฟฟ้ารวมในวงจรไฟฟ้านี้ โดยใช้กฎของโอห์ม (V = IR) ซึ่งจะได้ค่าเท่ากับ 3 A นั่นหมายถึงความยาวของแนวนอนแต่ละด้านส่วนสีขาว ดังภาพ
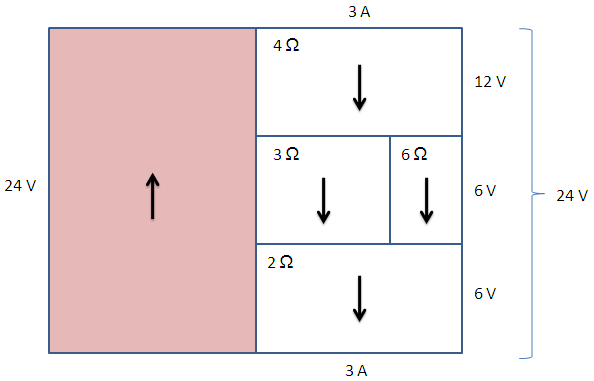
จากนั้น เราก็ค่อยมาคำนวณหาค่าความต่างศักย์ไฟฟ้าที่ตกคร่อมตัวต้านทาน 4 Ω และ 2 Ω ได้ ซึ่งจะได้ค่าเท่ากับ 12 V และ 6 V ตามลำดับ เนื่องจากค่าความต่างศักย์ไฟฟ้ารวมต้องมีค่าเท่ากับ 24 V ดังนั้น ค่าความต่างศักย์ไฟฟ้าที่ตกคร่อมตัวต้านทาน 2 ตัวที่ต่อขนานกัน (3 Ω และ 6 Ω) จึงต้องมีค่าเท่ากับ 6 V ดังภาพ
จากนั้น เราก็สามารถคำนวณหาค่ากระแสไฟฟ้าที่ผ่านตัวต้านทาน 3 Ω และ 6 Ω แต่ละตัวได้ ซึ่งจะได้ค่าเท่ากับ 2 A และ 1 A ตามลำดับ โดยผลรวมของ 2 ค่านี้ต้องมีค่าเท่ากับ 3 A ตามกฎของเคอร์ชอฟ ซึ่งก็เป็นเช่นนั่นจริงๆ ดังภาพ
เมื่อถึงตรงนี้ เราก็ทราบปริมาณต่างๆ ในวงจรไฟฟ้านี้หมดแล้ว แต่โจทย์ข้อนี้ถามว่า กำลังไฟฟ้าที่สูญเสียไปกับตัวต้านทาน 3 Ω มีค่าเท่าไร ซึ่งเราก็สามารถหาค่าได้โดยการนำค่ากระแสไฟฟ้าและค่าความต่างศักย์ไฟฟ้าที่ตกคร่อมตัวต้านทานนี้มาคูณกัน ซึ่งก็ได้ค่าเท่ากับ 12 W หรือก็คือพื้นที่ของสี่เหลี่ยมที่แทนตัวต้านทาน 3 Ω นั่นเอง [ยิ่งตัวต้านทานไหนกินพื้นที่มาก มันก็ยิ่งใช้กำลังไฟฟ้ามาก]
วิธีการนี้ช่วยนักเรียนได้มากนะครับ ในระหว่างที่นักเรียนกำลังคำนวณค่าอะไรก็แล้วแต่ ณ จุดใดๆ ของวงจรไฟฟ้า นักเรียนก็สามารถตรวจสอบได้ว่า ผลลัพธ์นั้นจะสอดคล้องกับส่วนอื่นๆ ของวงจรหรือไม่ ตรงนี้สำคัญเพราะว่า ในการวิเคราะห์วงจรไฟฟ้าใดๆ นักเรียนต้องมองภาพรวมทั้งหมดของวงจรไฟฟ้า ร่วมไปกับการมองภาพย่อยในแต่ละจุดในวงจรไฟฟ้านั้นไปพร้อมกันด้วยครับ